
『数学ガール』と『暗号技術入門』執筆時の手書きノート(4)で伝える工夫を学ぼう(本を書く心がけ)
※ほぼ半分を無料公開しているノートです。(結城メルマガVol.014より)
こんにちは、結城浩です。
「本を書く心がけ」のコーナーです。
このコーナーでは「本を書くこと」に関わるさまざまな話題をお話しします。
今日は「手書きノート」をお届けします。結城が本を書くときに手書きでノートやメモ帳に書いていたことを、スキャナでスキャンしてお見せし、何を考えていたのかを解説します。さらに、実際の書籍では結局どうなったのかの結末もお見せしましょう。
なお、他の「手書きノート」は以下でも公開していますので、ぜひご覧ください。
◆『数学ガール』執筆中の手書きノート(1)(本を書く心がけ)
https://note.mu/hyuki/n/n70104a303cdf
◆『数学ガール』を書いてるときの手書きノート(2)を公開します(本を書く心がけ)
https://note.mu/hyuki/n/n100ab6b1d5e0
◆『暗号技術入門』と『数学ガール』を書いてるときの手書きノート(3)を公開します(本を書く心がけ)
https://note.mu/hyuki/n/n414d3bf5841b
「手書きノート」がどんな意味を持つかは結城にもよくわからないのですが、文章を執筆なさる方(特に書籍執筆に関心のある方)には得るものが大きいと思っています。
さて、今日の「手書きノート」はどんなものでしょう。
●目次
・『暗号技術入門』を書いているときの手書きメモから:
・ブロック図で解説する
・「数学ガール」シリーズを書いているときの手書きメモから:
・立場の違いを考える
・ルールの見せ方と読者さんとのシンクロ
・三角関数は円関数
・数式と直感
●ブロック図で解説する
以下の「暗号化のブロック図(手書きメモ)」は、結城が『暗号技術入門』という書籍を書いているときに描いた図です。
◆暗号化のブロック図(手書きメモ)
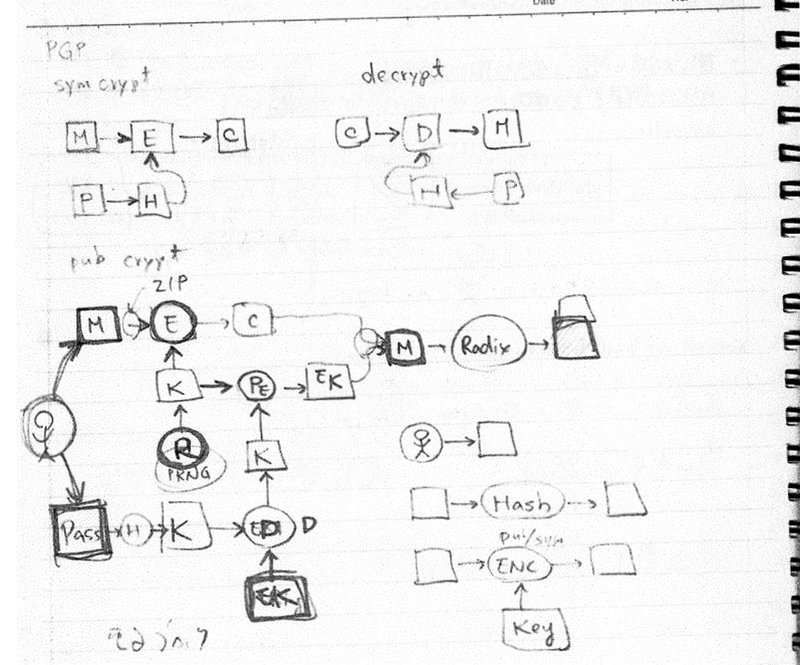
これはPGP (Pretty Good Privacy) という暗号ソフトウェアの動作を「ブロック図」を使って解説しようと検討しているところです。
図の上の方では対称暗号(慣用暗号)と呼ばれる方式の暗号の作り方、下の方では公開鍵暗号と呼ばれる方式の暗号の作り方を描いています。Mはメッセージ、Eは暗号化、Pはパスフレーズ、Hはハッシュ化をそれぞれ表しています。
見るからに複雑ですが、複雑だからこそ、このような「図」を使って説明する必要があるのですね。
現代の暗号技術は数学です。ですから、内容をきちんと表現するためにはどうしても数式が必要になります。しかし、『暗号技術入門』では読者層を考慮して、数式をできるだけ出さないようにする方針でした。そこで、数式を使う代わりに図を多用することにしました。暗号の仕組みや、ソフトウェアの構造を読者さんに理解してもらうために図をたくさん描いたのです。
この手書きメモを書きながら結城は、
「どんな図を描いたらわかりやすいかなあ」
と検討しているわけですが、それと同時に、
「自分は説明する内容を本当に理解しているか確かめよう」
という意図もあります。
この図は書籍になると、以下のようになります。
◆『暗号技術入門』(PGPの暗号化)
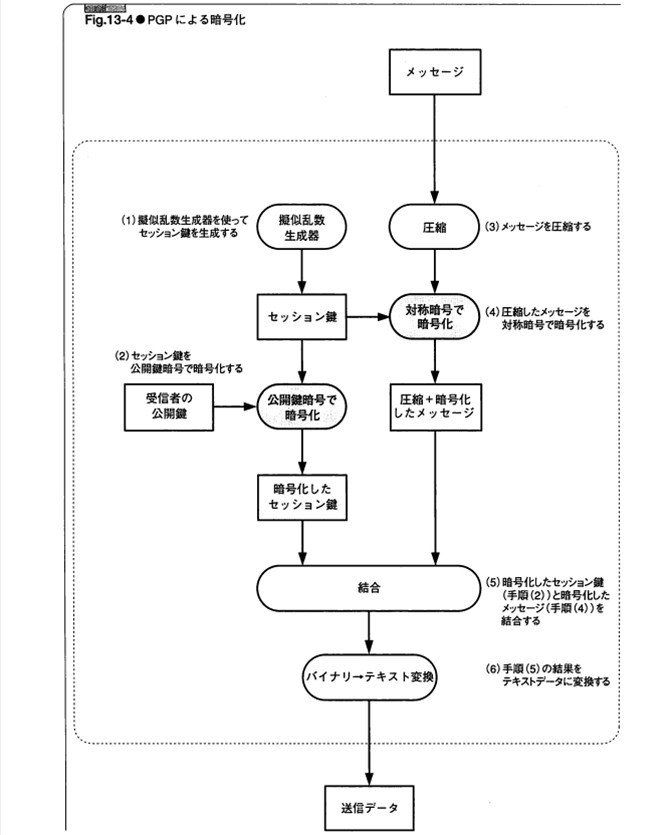
この図は、PGPの(公開鍵暗号を含んだ)暗号化の部分です。手書きメモでは「左から右に流れる図」を描いていましたが、書籍では「上から下に流れる図」に変更しました。これは、横長の図では縦長のページにうまく入らなかったからです。
結城は、グラデーションやシャドウのような「イフェクト」を図にかけることはあまりありません。ただし、「図に出てくる構成物は何を表しているか」だけは明確になるようにしています。
具体的に言いましょう。
この図に出てくる「メッセージ」や「セッション鍵」のような、「静的なデータ」は四角形で表現しています。それに対して、「圧縮」や「対称暗号で暗号化」のように、「動的な操作」は角が丸い四角形で表現しています。
さらに、PGPによる暗号化という「処理全体のまとまり」は破線で大きく括っています。このようにして、PGPによる暗号化に対する入力(メッセージ)と、出力(送信データ)が明確になるように工夫しています。
なお、この図はMicrosoft Visioというソフトウェアで描きました。Microsoft Visioは結城が長年愛用している描画ツールです。
◆Microsoft Visio 2010
http://www.amazon.co.jp/exec/obidos/ASIN/B003FZACDM/hyuki-mm-22/
●立場の違いを考える
さて、次に『数学ガール』を書いていたときの手書きメモをお見せします。以下の図は、ひとつの数列クイズに対して、
・数学が苦手なテトラちゃんという高校一年生
・数学が得意な「僕」という高校二年生、
・それに、数学がずばぬけて得意なミルカさんという高校二年生、
この三人がそれぞれにどのような反応をするかをメモしたものです。
◆『数学ガール』執筆メモ(手書きメモ)

このメモだけを見ても意味は取りにくいですね。
同じ数列を見ていても、見ている人物の「数学の理解度の違い」で答えは変化するだろう。だとしたら、誰がどのような答えをするだろうか…そんなことを考えていたときのメモです。
一般の物語では、登場人物がどのような性格をしているか(登場人物がどのような属性を持っているか)は、文章内の「描写」によって表現されます。
しかし、『数学ガール』のような数学物語では、登場人物の性格なり属性は、「数学の問題に対して、各人物がどのようなアプローチを取るか」によって表現されます。
答えを当てるだけの簡単な問題なら「どれだけ正解に近いか」によって人物の数学能力が推し量れます。
しかし、さまざまな答えの可能性がある問題なら、人物の数学に対するそれぞれの姿勢が、その答えに現れ、物語に豊かなふくらみをもたらしてくれます。登場人物はどのようなアプローチで問題に立ち向かうのか、どのような答えを良しとするのか…それを考えるのはとても楽しいものです。
この手書きメモでは、数学が非常によくできるミルカさんは「図形的な説明」まで踏み込んだ答えをするだろうな、といったメモを書いています。
この部分が実際の書籍になったらどうなるでしょう。以下がその書籍の部分です。
◆『数学ガール』(ド・モアブルの定理)

ここでは、ミルカさんがド・モアブルの定理に触れ、さらに、簡単ではありますが、図形的視点での解説を加えています。
ここで、ミルカさんの説明に注目してください。ミルカさんはド・モアブルの定理を「二つの表現」で述べています。
一つ目は、いわば数式の言い換えという形の表現で。
《複素数cosθ+isinθをn乗すると複素数cos nθ+ isin nθになる》
二つ目は、図形的視点での表現で。
《単位円上でθの回転をn回繰り返すのは、nθの回転に等しい》
ひとつの事柄を、二つの表現を使って表すのはとても大切です。
二つの表現で説明された文章を読むことで、読者は自分の理解を確かなものにすることができます。さらに読者はある種の「驚き」を得ることもあるでしょう。すなわち、
「自分はよくわかっていると思ってた。でも、そんな見方もできるのか! 確かにそうだね!」
という「驚き」です。これは読者によっては大きな感動へつながります。
そういえば、結城メルマガのVol.010で、
「教えるときの二刀流」
というお話をしました。それに通じるものがあります。
※ここまででおおよそ半分です。もし「先を読みたい」と思った方はぜひご購入をお願いします。
続きをみるには
¥ 200
いただいたサポートは、本やコンピュータを買い、さまざまなWebサービスに触れ、結城が知見を深める費用として感謝しつつ使わせていただきます! アマゾンに書評を書いてくださるのも大きなサポートになりますので、よろしくお願いします。 https://amzn.to/2GRquOl

